Domain-specific Circuits

Designing efficient devices and circuits with novel functionalities often involves mapping unique features of underlying materials directly to applications. Using this notion of natural computing where intrinsic physics matches desired functionality, we design and prototype domain-specific, mixed-signal circuits that can be much more efficient than conventional approaches. When appropriate, we explore possibilities of emulations of emerging technology-based circuit and device concepts through microprocessor (Arduino), FPGA and mixed-signal ASIC implementations in order to gauge the scalability of these emerging technologies.

A compact Binary Stochastic Neuron

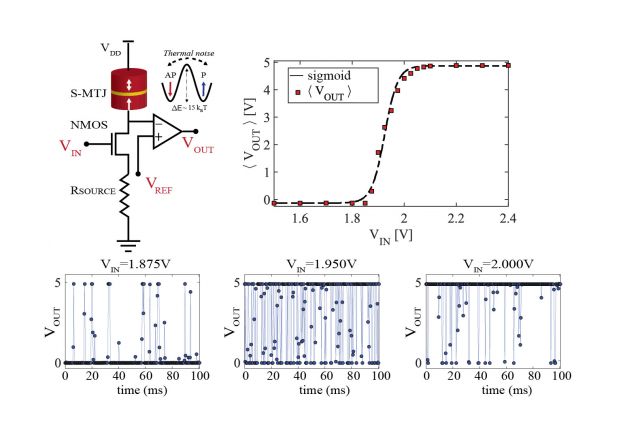
A striking example of a domain-specific building block is the hardware implementation of a binary stochastic neuron (BSN) with a single noisy resistor, an unstable magnetic tunnel junction (MTJ) plus a couple of transistors. The BSN lies at the heart of stochastic neural networks such as Boltzmann Machines and Belief Nets and as such BSNs can be used as computational primitives for combinatorial optimization, inference and learning tasks. The BSN is a mixed-signal unit: Its input is the analog transistor voltage that controls the steady-state probability of the random bitstream, while the output is digital, always 0 or 1 with a given probability. Implementing such a tunable random unit using conventional design poses many challenges.

• How does one get a truly random seed?
• Even if pseudo-random generation (PRNG) is adequate, how does one ensure that the PRNG has a long enough period to avoid unwanted correlations?
• How does one get the controllable tunability of the output?

While it is impossible to rule out creative approaches, our earnest answer to these questions led us to the conclusion that implementing the same function requires more than a 1000 transistors in digital circuits compared to the 3 transistors and a single MTJ used in the mixed-signal design.

Optimization using BSNs

The key feature of BSNs is not in their random behavior, but rather in the tunability of their randomness. Tunability allows BSNs to get correlated with one another and when the interconnections are adjusted properly, the system of BSNs can naturally lead to low energy (minimum cost) states of a desired problem. Optimization functions with such discrete variables (sometimes called combinatorial optimization problems) are ubiquitous in real-world applications, most notably in Machine Learning. Indeed, many different types of natural "annealers" in hardware have been developed over the years. The compactness of the BSN design and the enormous advances in the memory technology based on MTJs that have put about a billion of them in a single chip suggest that there could be massively-scaled natural annealers that make use of thermal noise in the environment. Having said that, we are actively looking for alternative designs that use different physical phenomena (other than thermally generated magnetic noise) to implement better, more scalable BSNs.

Factorization as Optimization

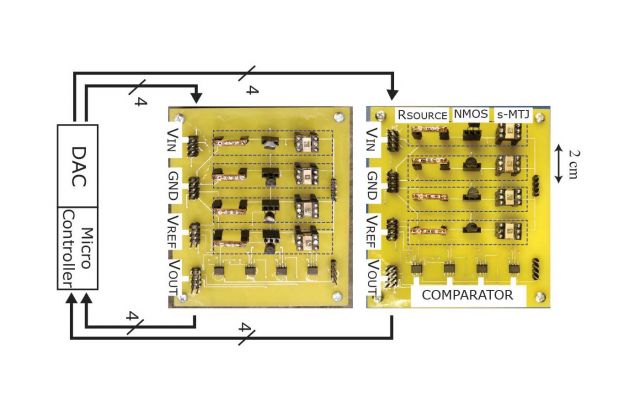
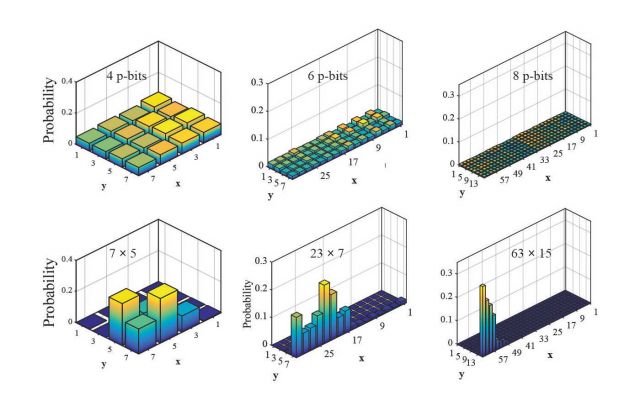
So how does the interconnected BSNs perform natural optimization? First, as commonly done in Machine Learning contexts, a cost function is identified. Then the appropriate interconnection matrix (sometimes called the weight matrix) is obtained to couple the BSNs to each other. In the circuit above, this is achieved by a microcontroller though in eventual implementations the interconnection matrix could be a resistive (or memristive) crossbar to perform a weighted summation of BSN outputs. Then the system is calibrated to produce a random probability distribution when the BSNs are disconnected. After the calibration step, the interconnections are turned on and the BSNs start listening to each other in a way to reach a consensus that lowers the cost function. After a while when enough samples are taken, a probability histogram can be taken to show the low energy (and high probability) states of the system are visited more often. In the case of factorization, the low energy states correspond to factors of a predefined factor, but the choice of integer factorization is incidental: The cost function can correspond to many other combinatorial optimization instances where a set of discrete variables minimizes the cost that is linked to a problem of interest.

What is Next?

The use of noisy magnetic tunnel junctions to implement a complicated function is just a representative example of domain-specific devices and circuits. After all, BSN is an abstraction that can be implemented using conventional technology, albeit with higher area and energy-efficiency requirements, at least in purely digital form. We are constantly on the lookout for phenomena or new materials that we can use to provide complicated functionalities that do not come naturally to standard methods.

In this regard, there are two independent threads we are pursuing:

• Scaling up the mixed-signal circuits: What is shown as an example here is a circuit with only 8 units while the memory industry have managed to mass produce chips with 1 billion such devices in them. As such, we believe that there is an intriguing opportunity to repurpose memory chips of the STT-MRAM industry to deliver supercomputer performance by natural annealers that can run on a laptop.
• Exploring alternative phenomena: Physicists and engineers have long observed different incarnations of random noise in different contexts. We are actively exploring other types of noise can be used to efficiently implement probabilistic computers of the future with better hardware scaling and unique features.