Physics-based Modeling

We seek to translate emerging materials and phenomena (from the fields of nanoelectronics, spintronics, magnetism among others) into physics-based circuit models that can be used to design benchmark circuits. These benchmarks then lead to behavioral models for higher level design. We work closely with experimentalists to calibrate models that are obtained in combination with available experiments and theoretical tools, sometimes starting from first principles techniques (quantum transport by NEGF methods) and sometimes from phenomenological models (semiclassical transport, spin-diffusion, statistical mechanics-based models).

Spins and Magnets

Making electron devices that use the spin degree of freedom of electrons in addition to their charge has become a powerful field of its own, now called spin electronics or shortly spintronics. The field of spintronics has led to the commercialization of new types of memory devices that combine spins and magnets. Beyond better and more efficient memory devices, the interplay between spin currents and magnets can lead to new types of information processing devices. A robust understanding of the interaction between spin currents and magnets is crucial for evaluating new devices and circuits. Our approach to modeling spintronic circuits has been to introduce physics-based, SPICE-compatible and reusable modules that are connected to microscopic theories of transport including spin-diffusion and quantum transport models. These transport circuits are then combined with models that account for magnetization dynamics, often described by macrospin or micromagnetics models. Once transport and magnetics models are represented as electronic circuits, they can be combined with state-of-the-art transistor models for accurate device and circuit level evaluation.

Modularity is Not Obvious

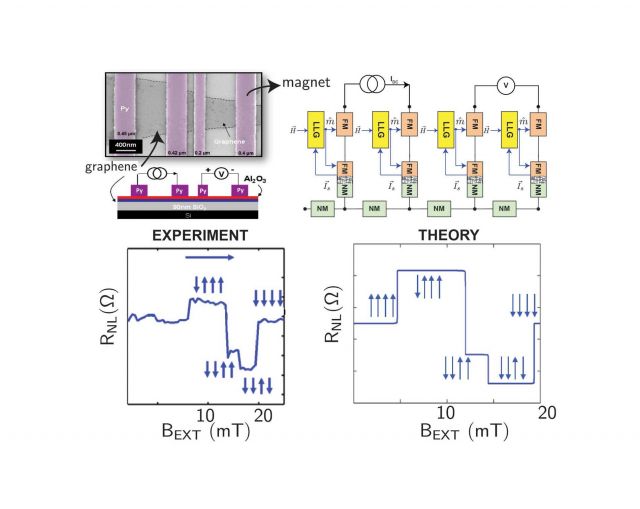
Such a modularity that decouples interfaces from channels is far from obvious. Just as one cannot naively assemble a p-n junction by putting together a p-type resistor and an n-type resistor − we would end up with two resistors in series and not a rectifier − one cannot build a spin-valve by attaching two magnets as ordinary conductances. What allows modularity is the use of generalized voltages and currents that explicitly account for spin and charge transport, much like separate quasi-Fermi levels that separately account for holes and electrons semiconductors. In this view, even the simplest resistor that relates a charge voltage to a charge current becomes a 4 x 4 conductance matrix that relates a 4 x 1 voltage vector (1 charge + 3 spin voltages) to their respective currents, also represented as 4 x 1 vectors. On the top right is an example of how this SPICE-compatible circuit approach can be used to build experimental structures out of elemental modules. Such composite spin-circuits reproduce known theory in simpler geometries and in addition they can flexibly be combined to capture non-trivial features of experiments with complicated structures. The example shown is a non-local spin-injection experiment into graphene where the measured voltages across the voltage probes change depending on the orientation of magnets.

Growing List of Spintronic Materials and Phenomena

The field of spintronics has been progressing very rapidly with discovery of new materials and phenomena at a very fast pace. Over the years, we have developed spin-circuit models to include a good portion of these developments. Keeping up with the field is a moving target that we actively pursue, since developing physics-based, experimentally benchmarked and robust models that can be combined with one another requires care and typically it takes one paper to do just that, to come up with a circuit model for a new material or effect. Depending on the degree of maturity and understanding the depth and details of models also vary. For example the ferromagnet-normal metal interface has a deep theoretical background based on microscopic theory (first developed by Bauer, Brataas and Kelly) that is reflected in its 4-component formulation, while emerging fields such as voltage-control of magnetism might involve more phenomenological models in the beginning.

Spin-circuits are Not Compact Models

An important distinction needs to be made between spin-circuit models and industry-grade compact models for modern transistors. Compact models often involve many fitting parameters with much more detail to accurately describe device characteristics. They are built and maintained for devices that are in a much more mature stage of development that can be considered as final models. Spin-circuits of the type we discuss here rather are first models for emerging materials and phenomena and their value is in their robust connection to underlying microscopic theory. Such a strong connection is often unnecessary and unwieldy for industrial compact models but is essential in approximately evaluating device, circuit and system-level implications of emerging technology that is in relatively immature stages of development.

Beyond Spin Transport

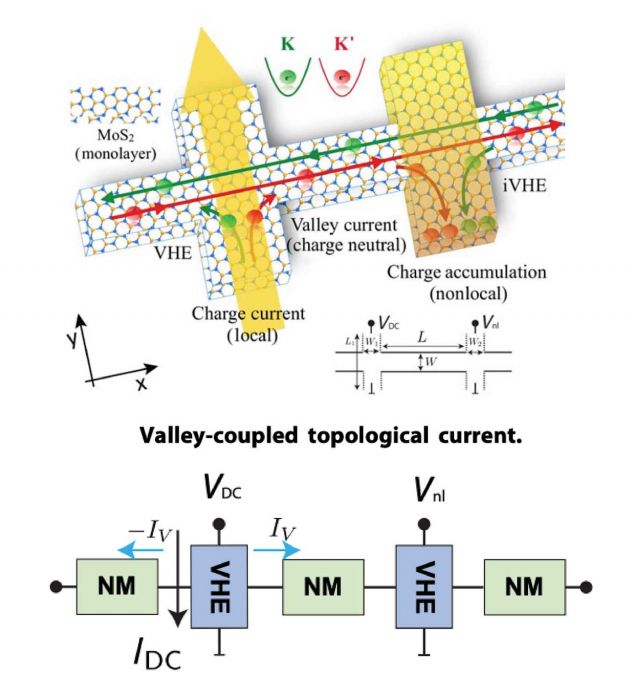
The strong connection of spin-circuits to underlying microscopic theories allows them to be carried over to different domains. An example of this is the application of the same spin-circuit models to valley transport where electron transport distinguishes different valleys of electronic bandstructure. Because valley diffusion is mathematically similar to spin diffusion, spin-circuit models that were originally developed for spin transport can be readily used to understand valley transport. Using these spin transport models, we were able to extend known theoretical results for valley diffusion into high valley-Hall effect regimes without making any modifications to our existing models.

Along the same lines, we are constantly exploring ways to extend the library of spin-circuits to accelerate device and circuit level analysis of emerging materials and phenomena to streamline their evaluation in hybrid systems involving existing technology.